矩阵点乘和叉乘的主要区别如下一结果类型不同 点乘内积矩阵或向量的点乘计算得到的结果是一个标量这个标量表示了两个向量在方向上的相似程度，也可以理解为两个向量夹角的余弦值乘以它们的模的乘积叉乘外积矩阵特指三维矩阵或向量的叉乘得到的结果是一个向量这个向量垂直于原两个向量所构成的平面，并且其方向符合右手定则。

叉车和点乘的区别是定义性质用途运算方式1定义 叉乘Cross Product是向量运算的一种，表示为×，用于描述平面内的旋转和方向点乘Dot Product也是向量运算的一种，表示为#8226，用于描述两个向量之间的角度和长度关系2性质 叉乘的结果是一个向量，该向量垂直于作为运算输入的两。

点乘和叉乘的区别主要体现在以下几个方面定义与结果点乘是向量的内积，结果是一个标量它表示一个向量在另一个向量方向上的投影长度叉乘是向量的外积，结果是一个向量这个新向量与原有的两个向量都垂直几何意义点乘在图形学中，点乘常用于判断两个向量是否垂直同时，也可以用来计算。

1 点乘和叉乘在表示意义上有所不同点乘指的是向量的内积，而叉乘则是指向量的外积2 它们的结果单位不同点乘的结果是一个标量，即一个向量在另一个向量方向上的投影长度叉乘的结果是一个向量，它与原来的两个向量都垂直3 计算方法也有所区别点乘的计算公式为 a * b = a *。

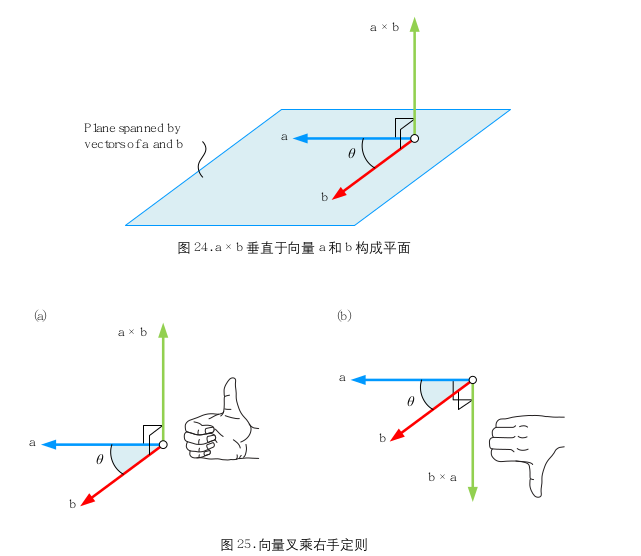
值得注意的是，叉乘的方向遵循右手定则，即a×b与向量a和b都垂直，且aba×b三者构成右手系如果向量a和b是平行的，那么叉乘的结果将是一个零向量这是因为平行向量的夹角为0度或180度，正弦值为0，因此叉乘的结果为零向量总的来说，点乘和叉乘都是向量运算的重要组成部分，各自具有独特的。